Heisenberg's Uncertainty Principle

Image from the article
"Quantum computers could overturn Heisenberg’s uncertainty principle".
Credit: io9

In quantum mechanics, the uncertainty principle is any of a variety of mathematical inequalities asserting a fundamental limit to the precision with which certain pairs of physical properties of a particle, such as position x and momentum p, can be known simultaneously. The more precisely the position of some particle is determined, the less precisely its momentum can be known, and vice versa. The original heuristic argument that such a limit should exist was given by Werner Heisenberg in 1927, after whom it is sometimes named, as the Heisenberg principle. A more formal inequality relating the standard deviation of position σ_x and the standard deviation of momentum σ_p was derived by Earle Hesse Kennard later that year (and independently by Hermann Weyl in 1928),

where ħ is the reduced Planck constant.

in wikipedia

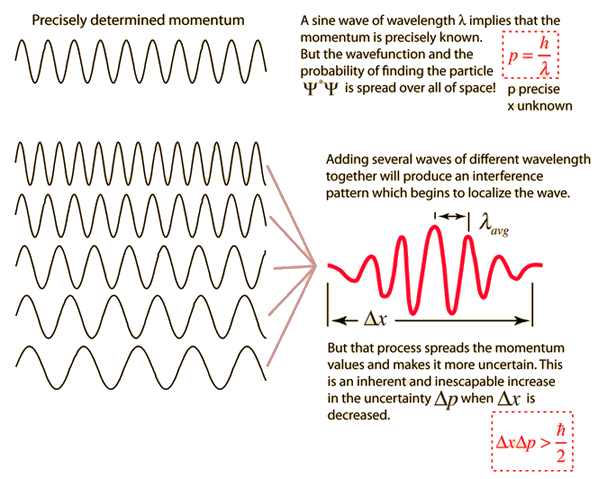Graphical interpretation of the Uncertainty Principle. Credit: hiperphysics

The first formulation of the uncertainty principle. In its present form it is an epistemological principle, since it limits what we can know about the electron. From "elementary formulae of the Compton effect" Heisenberg estimated the ‘imprecisions’ to be of the order

δpδq ∼ h               (1)

The first mathematically exact formulation of the uncertainty relations is due to Kennard. He proved in 1927 the theorem that for all normalized state vectors |ψ> the following inequality holds:

Δψp Δψq ≥ ℏ/2       (2)

where, Δ_ψp and Δ_ψq are standard deviations of position and momentum in the state vector |ψ>.

Since the above inequalities have the virtue of being exact and general, in contrast to Heisenberg's original semi-quantitative formulation, it is tempting to regard them as the exact counterpart of Heisenberg's relation (1). Indeed, such was Heisenberg's own view. In his Chicago Lectures (Heisenberg 1930, pp. 15-19), he presented Kennard's derivation of relation (2) and claimed that "this proof does not differ at all in mathematical content" from the semi-quantitative argument he had presented earlier, the only difference being that now "the proof is carried through exactly".

So, the above inequalities as showing that the formalism is consistent with Heisenberg's empirical principle.

This situation is similar to that arising in other theories of principle where one often finds that, next to an empirical principle, the formalism also provides a corresponding theorem. And similarly, this situation should not, by itself, cast doubt on the question whether Heisenberg's relation can be regarded as a principle of quantum mechanics.

There is a second notable difference between (1) and (2). Heisenberg did not give a general definition for the ‘uncertainties’ δp and δq. The most definite remark he made about them was that they could be taken as "something like the mean error". In the discussions of thought experiments, he and Bohr would always quantify uncertainties on a case-to-case basis by choosing some parameters which happened to be relevant to the experiment at hand.

adapted from http://plato.stanford.edu/entries/qt-uncertainty/