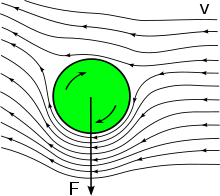
The Magnus effect is the phenomenon whereby a spinning object flying in a fluid creates a whirlpool of fluid around itself, and experiences a force perpendicular to the line of motion.
In fluid dynamics, Bernoulli's principle states that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy. But it doesn't mention the effect when an object is spinning through a fluid (that's what happened in Magnus effect), that has an incremental energy due to the spinning object.
Principle
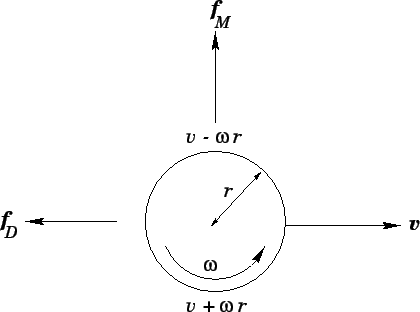
When a body (such as a sphere or circular cylinder) is spinning in a viscous fluid, it creates a boundary layer around itself, and the boundary layer induces a more widespread circular motion of the fluid. One explanation of the Magnus effect is since there is more (forward) acceleration of air on the forward-moving side than the backward-moving side, there is more pressure on the forward-moving side, resulting in a perpendicular component of force from the air towards the backward-moving side (watch the video bellow).
Calculation of Magnus force
Given the angular velocity vector  and velocity
and velocity  of the object, the resulting force
of the object, the resulting force  can be calculated using the following formula:
can be calculated using the following formula:
 and velocity
and velocity  of the object, the resulting force
of the object, the resulting force  can be calculated using the following formula:
can be calculated using the following formula:
where S is dependent on the average of the air resistance coefficient across the surface of the object.[8] The  denotes the vector cross product.
denotes the vector cross product.
 denotes the vector cross product.
denotes the vector cross product.
An example of spin ball in the air
The following equation demonstrates the lift force induced on a ball that is spinning along an axis of rotation perpendicular to the direction of its translational motion:
- F = lift force
- ρ = density of the fluid
- r = radius of the ball
- v = velocity of the ball
- A = cross-sectional area of ball
- CL = lift coefficient
The lift coefficient CL may be determined from graphs of experimental data using Reynolds numbers and spin ratios.[9] For a smooth ball with spin ratio of 0.5 to 4.5, typical lift coefficients range from 0.2 to 0.6.




No comments:
Post a Comment