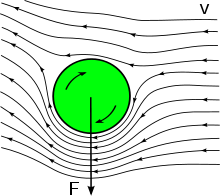
The Magnus Force

The Magnus effect, demonstrated on a ball. v represents the wind velocity, the arrow F the resulting force towards the side of lower pressure. (from: wikipedia)

The Magnus effect is the phenomenon whereby a spinning object flying in a fluid creates a whirlpool of fluid around itself, and experiences a force perpendicular to the line of motion.
In fluid dynamics, Bernoulli's principle states that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy. But it doesn't mention the effect when an object is spinning through a fluid (that's what happened in Magnus effect), that has an incremental energy due to the spinning object.

Principle

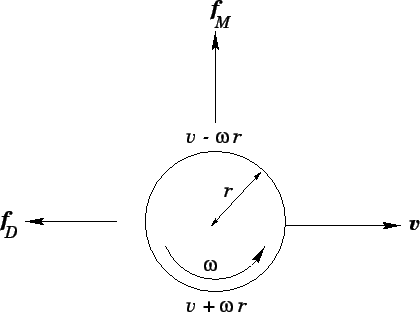
When a body (such as a sphere or circular cylinder) is spinning in a viscous fluid, it creates a boundary layer around itself, and the boundary layer induces a more widespread circular motion of the fluid. One explanation of the Magnus effect is since there is more (forward) acceleration of air on the forward-moving side than the backward-moving side, there is more pressure on the forward-moving side, resulting in a perpendicular component of force from the air towards the backward-moving side (watch the video bellow).

Calculation of Magnus force

Given the angular velocity vector  and velocity  of the object, the resulting force  can be calculated using the following formula:

where S is dependent on the average of the air resistance coefficient across the surface of the object.^[8] The  denotes the vector cross product.

An example of spin ball in the air

The following equation demonstrates the lift force induced on a ball that is spinning along an axis of rotation perpendicular to the direction of its translational motion:

F = lift force

ρ = density of the fluid

r = radius of the ball

v = velocity of the ball

A = cross-sectional area of ball

C_L = lift coefficient

The lift coefficient C_L may be determined from graphs of experimental data using Reynolds numbers and spin ratios.^[9] For a smooth ball with spin ratio of 0.5 to 4.5, typical lift coefficients range from 0.2 to 0.6.

Fonts: wikipedia; utexas; aviation-for-kids;